
This puzzle, courtesy of www.wtharvey.com, is from the game Lahno-Etmans, Wijk aan Zee 2004.
White wins beautifully with 1.Qf7+ Kh4 2.Rd4+ Qxd4 3.g3#.





 Here is our starting crosstable, before we've added any details.
Here is our starting crosstable, before we've added any details. 2. Clue #2 tells us that Ann's only win came against Bill, so we know that Dan either drew with Ann or defeated her. We also know from clue #4 that Dan lost exactly two games. Since the crosstable already shows Dan's game with Bill ending in a tie, his only remaining games, with Chris and Ed, must be losses.
2. Clue #2 tells us that Ann's only win came against Bill, so we know that Dan either drew with Ann or defeated her. We also know from clue #4 that Dan lost exactly two games. Since the crosstable already shows Dan's game with Bill ending in a tie, his only remaining games, with Chris and Ed, must be losses. 4. Clue #1 tells us that Ed had the same result against Ann as he did against Chris. We know already that his game against Ann must have been a draw or a win. But if his game against Ann was a win, then from clue #1 this would mean he also defeated Chris. But this would give him a total of at least 3 points and we know (from clue #3) that he only scored 2 points total. Therefore, his games against Ann and Chris must both have been draws. This also means that Ed must have lost to Bill in order for Ed to total 2 points for the tournament. Now our crosstable looks like this:
4. Clue #1 tells us that Ed had the same result against Ann as he did against Chris. We know already that his game against Ann must have been a draw or a win. But if his game against Ann was a win, then from clue #1 this would mean he also defeated Chris. But this would give him a total of at least 3 points and we know (from clue #3) that he only scored 2 points total. Therefore, his games against Ann and Chris must both have been draws. This also means that Ed must have lost to Bill in order for Ed to total 2 points for the tournament. Now our crosstable looks like this: 5. We're almost done now. Clue #8 tells us that Bill had the same result against Ed as Dan did against Ann. Since Bill defeated Ed, this means that Dan also won against Ann. The last bit of information we need comes from clue #6, that at least four games were drawn. Since we only show three draws so far, the remaining game (Ann vs. Chris) must have been a draw. We can now complete our crosstable:
5. We're almost done now. Clue #8 tells us that Bill had the same result against Ed as Dan did against Ann. Since Bill defeated Ed, this means that Dan also won against Ann. The last bit of information we need comes from clue #6, that at least four games were drawn. Since we only show three draws so far, the remaining game (Ann vs. Chris) must have been a draw. We can now complete our crosstable: So Chris won the tournament with 3 points, Ann and Ed tied with 2 each, and Bill and Dan brought up the rear with 1.5 points each.
So Chris won the tournament with 3 points, Ann and Ed tied with 2 each, and Bill and Dan brought up the rear with 1.5 points each.
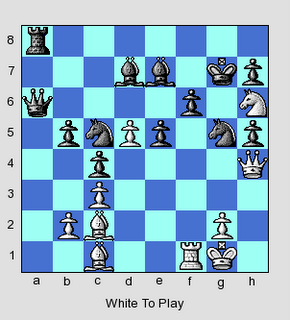
 This problem is from Korneev-Zelcic, 2005 European Championship, Warsaw, after 31... Rxg2. The game continued 32.Qxe6+ Nd7 33.Qe8+ Kc7 34.Bf4+ Kb6 35.c5+ Ka6 36.Bc4+ Ka5 37.Bd2+ Rxd2 38.Qxg6 1-0.
This problem is from Korneev-Zelcic, 2005 European Championship, Warsaw, after 31... Rxg2. The game continued 32.Qxe6+ Nd7 33.Qe8+ Kc7 34.Bf4+ Kb6 35.c5+ Ka6 36.Bc4+ Ka5 37.Bd2+ Rxd2 38.Qxg6 1-0.